A Binary Search Tree (BST) is a binary tree where the nodes are ordered following these characteristics:
- The left subtree of a node contains only nodes with values lower than the node’s value
- The right subtree of a node contains only nodes with values greater than the node’s value
- The left and right subtree each must also be a Binary Search Tree
- There must be no duplicate values
- A unique path exists from the root to every other node
The possible operations on a Binary Search Tree are: Search, Insert and Delete. An update is just a delete followed by an insert.
Binary Search Trees are pretty easy to implement and let you insert, delete and search in O(n) in the worse case scenario. There are self-balancing Binary Search Trees, that are harder to implement but offer O(log n) performance. I’m not going to cover self-balancing trees in this post.
Search
Searching a Binary Search Tree follows these steps:
- Grab the root node and check the value
- If that’s the value you are looking for, then we are done
- If the value you are looking for is greater, then do a search on the right node
- If the value you are looking for is lower, then do a search on the left node
- If at any time you find a null node, then the value is not in the tree
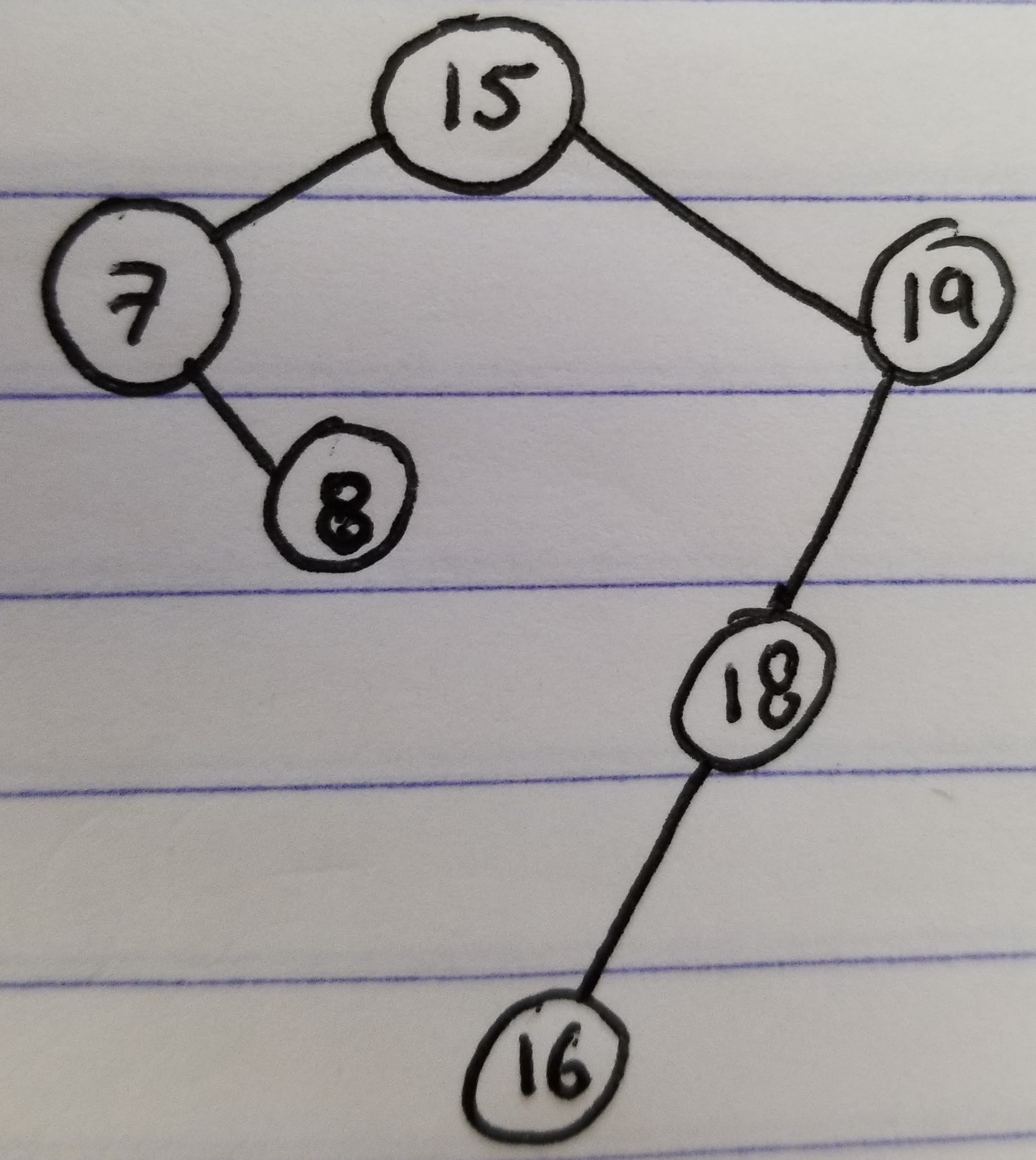
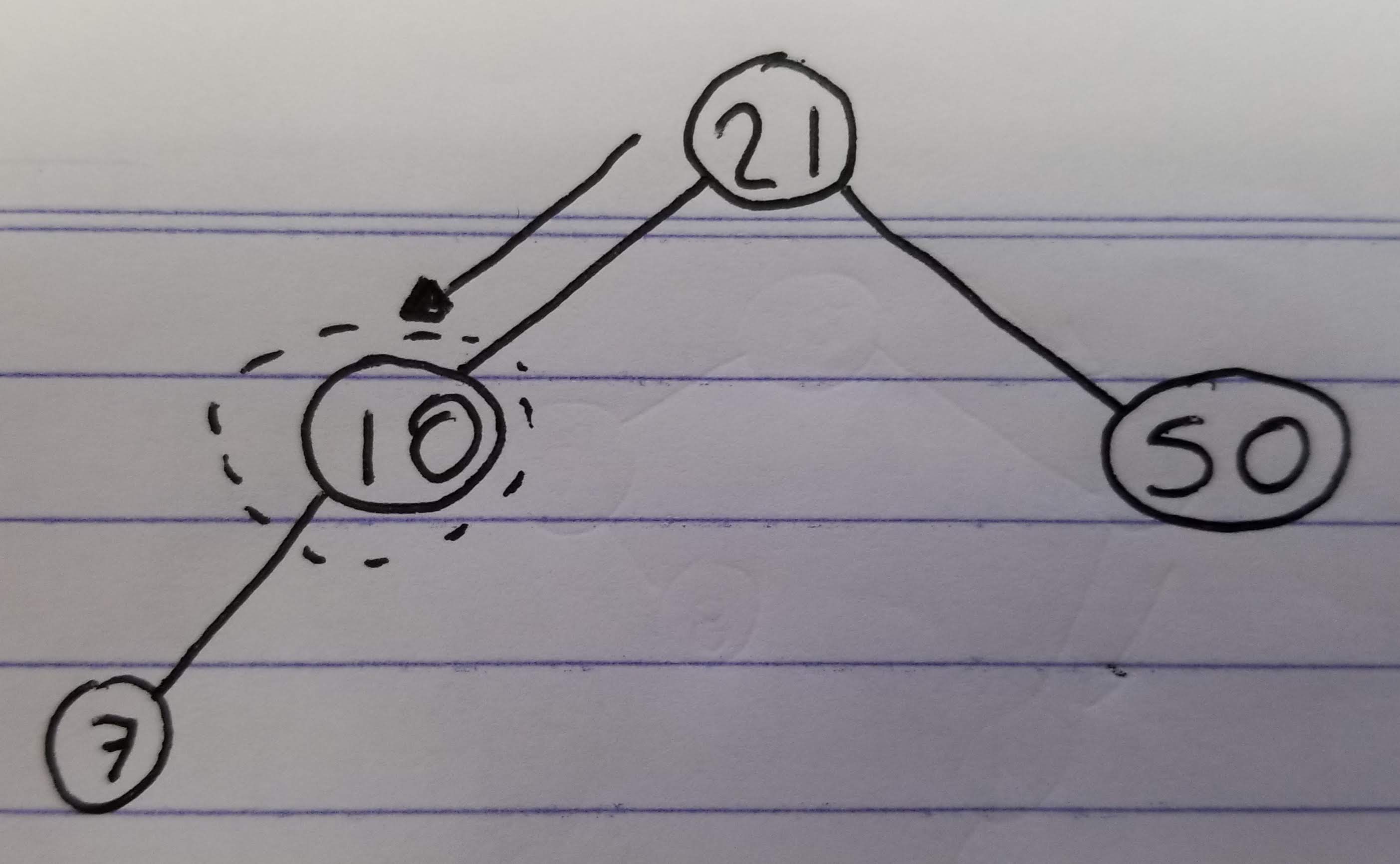
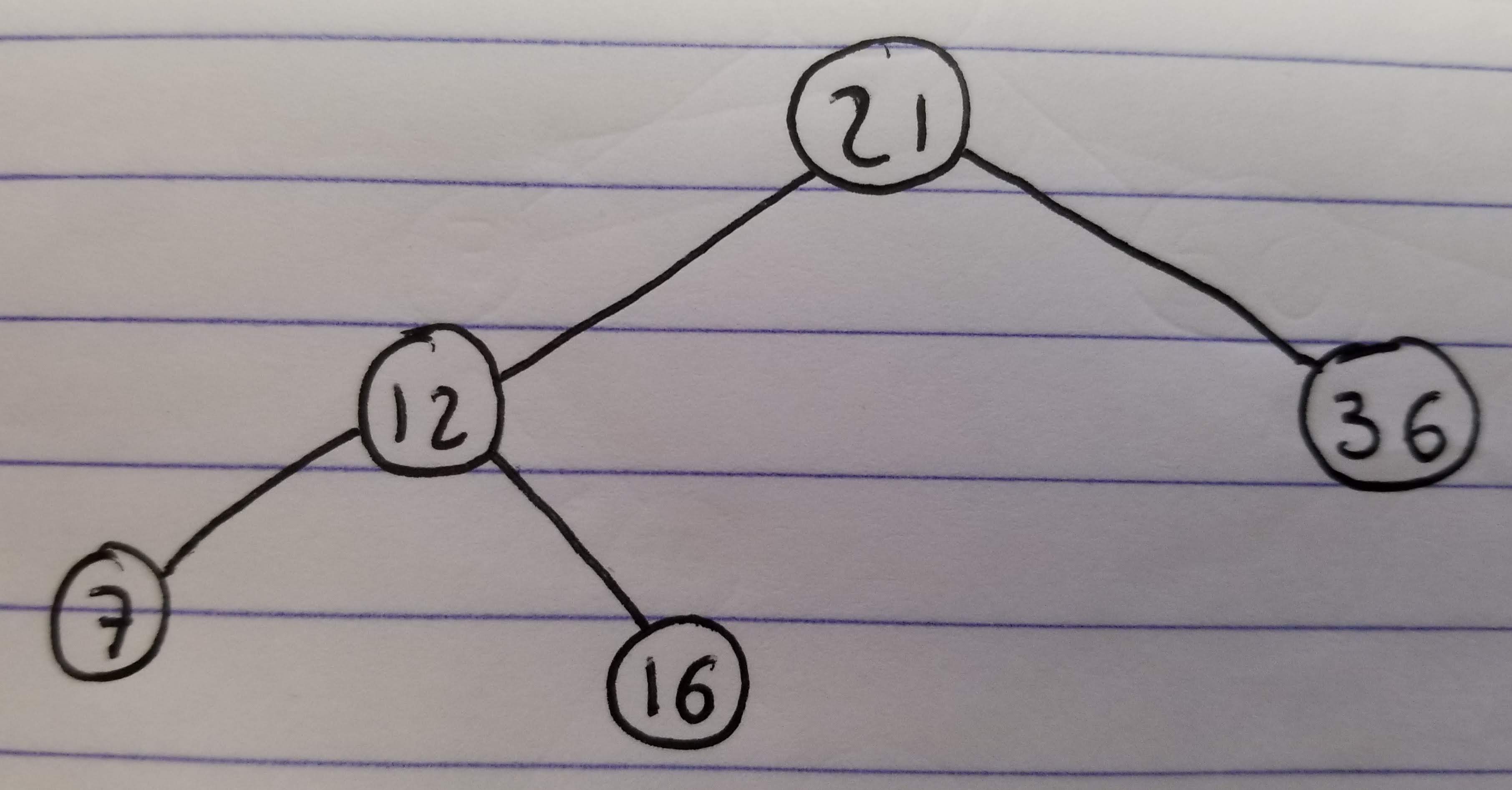
Consider a tree like this:
If we search for value 18 on that tree, we will follow these steps:
- Start at the root
15is not the value we are looking for,we move to the right child19is not the value we are looking for, we move to the left child18is the value we are looking for, we are done
Insert
Inserting in a Binary Search Tree is very similar to the search:
- Follow the same procedure as search
- If the value is found, then there is nothing to do
- If the value is not found, we are going to create a new node as a child of the last node in the search chain
- If the value to insert is higher than the last node, we’ll insert a new node as a right child
- If the value to insert is lower than the last node, we’ll insert a new node as a left child
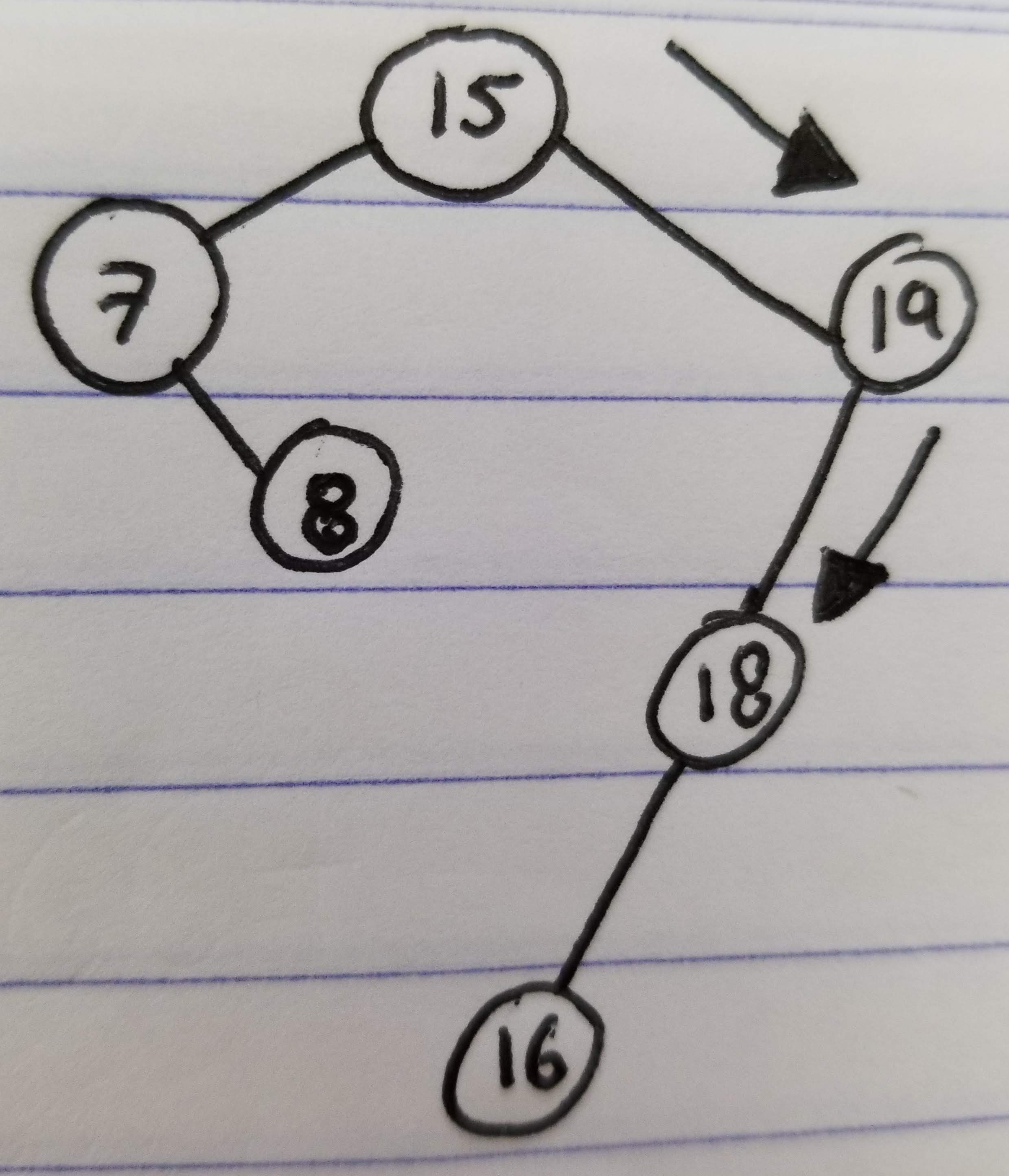
The image above, illustrates the steps to insert a value in a binary tree:
- A search for value
19is done in the tree 16is the last node in the search (Since19is greater, but there is no right child)- We create a new node with value
19and add it as right child of16
Delete
Deleting is a little harder to implement. It follows these steps:
- Find the node you want to delete (Let’s call it A)
- If it’s not found, there is nothing to do
- If A doesn’t have any children, just delete it (Unlink it from the parent)
- If A has a single child (Let’s call it B), link A’s parent to B, instead of A. A will no longer be a part of the tree
- If A has two children, find the lowest element on it’s right subtree. This can be done by going to A’s right child (Let’s call it B) and then going down to the left child, until there are no more left children (Let’s call this last node on the left, C).
- Set the value of A to the value C
- Delete node C (C will be a leaf, or have only a right child, so one of the techniques from above can be used)
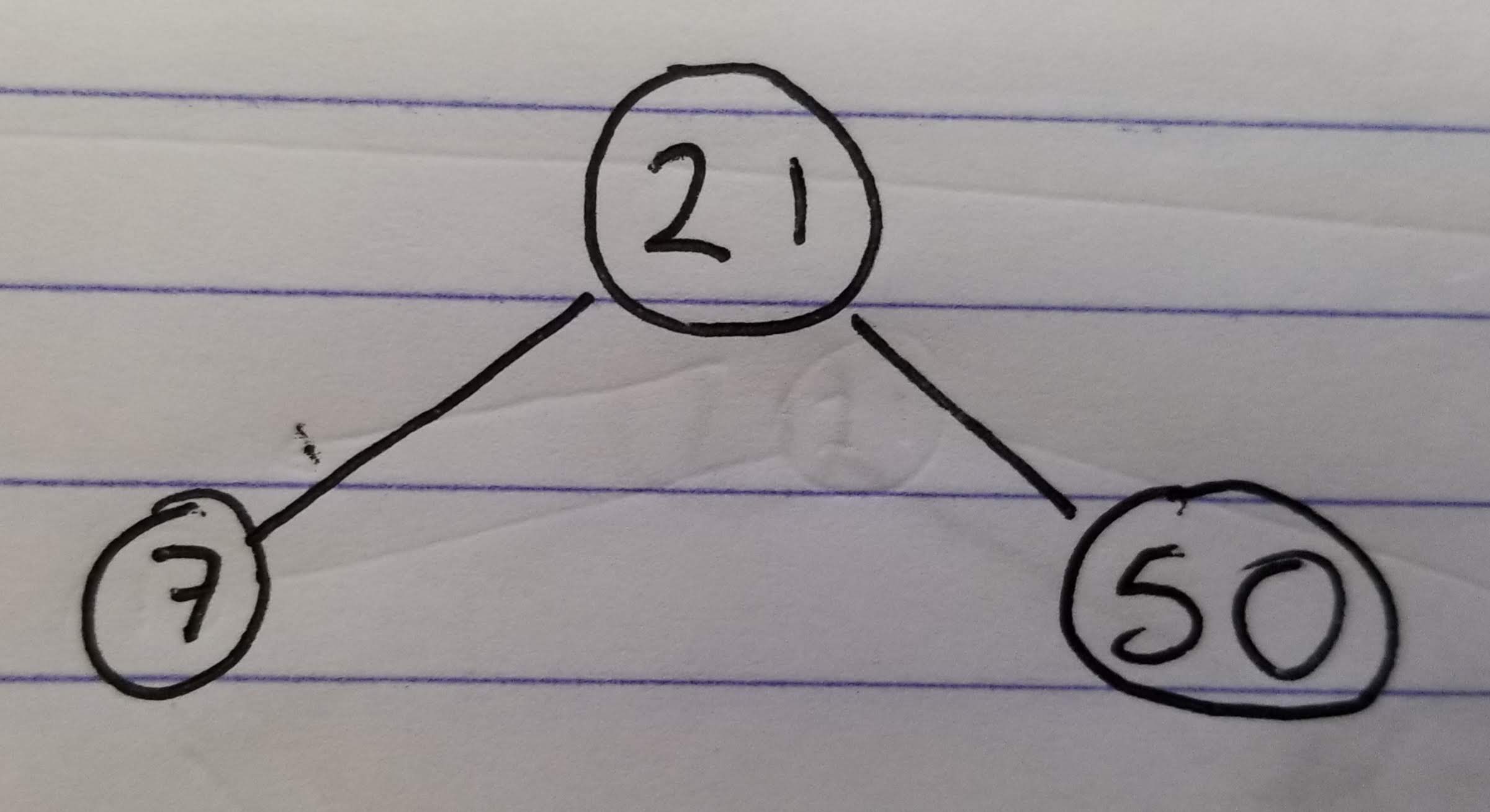
The simplest case would be deleting a leaf:
- Find node
19 - Remove the node (Set
16’s right child to null)
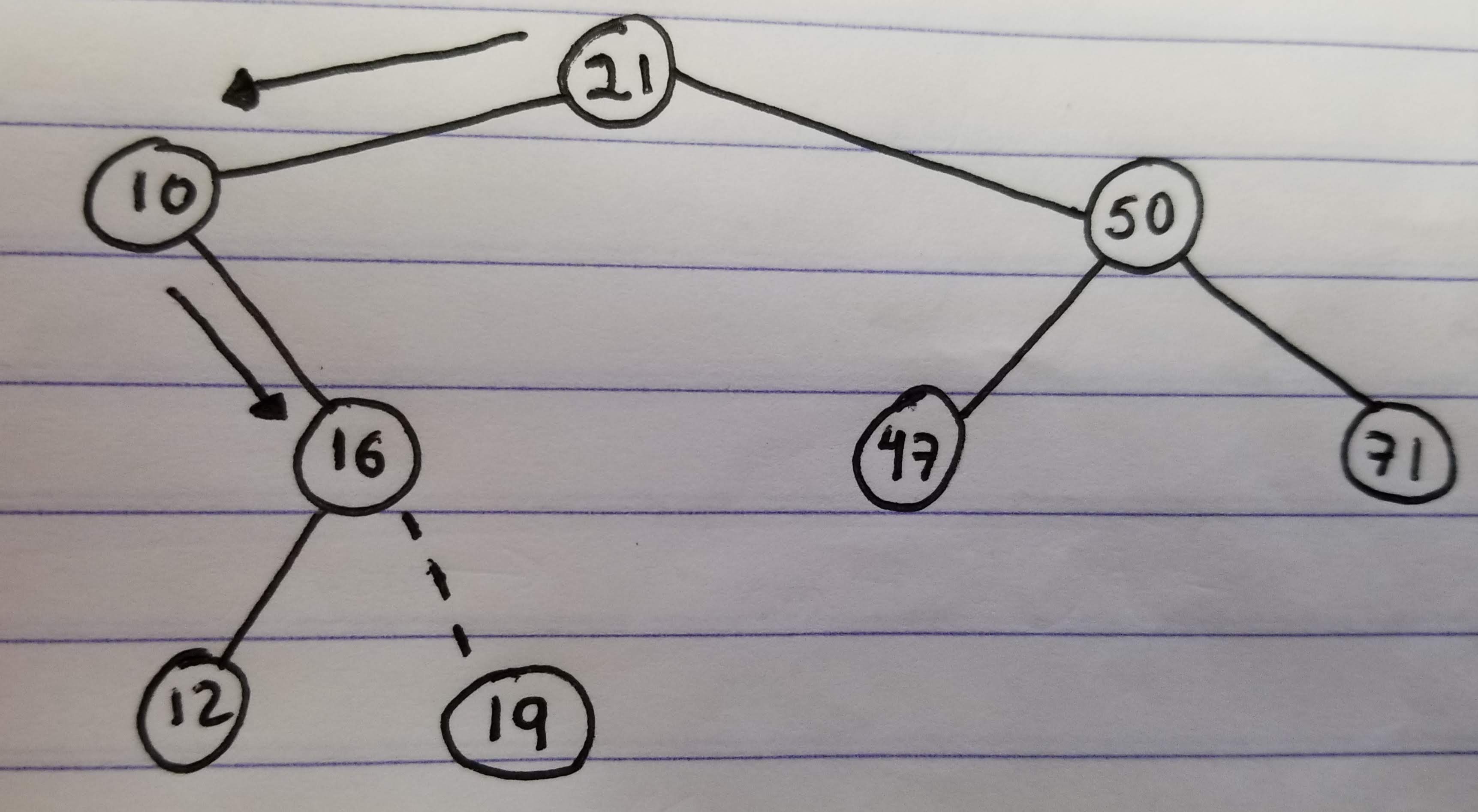
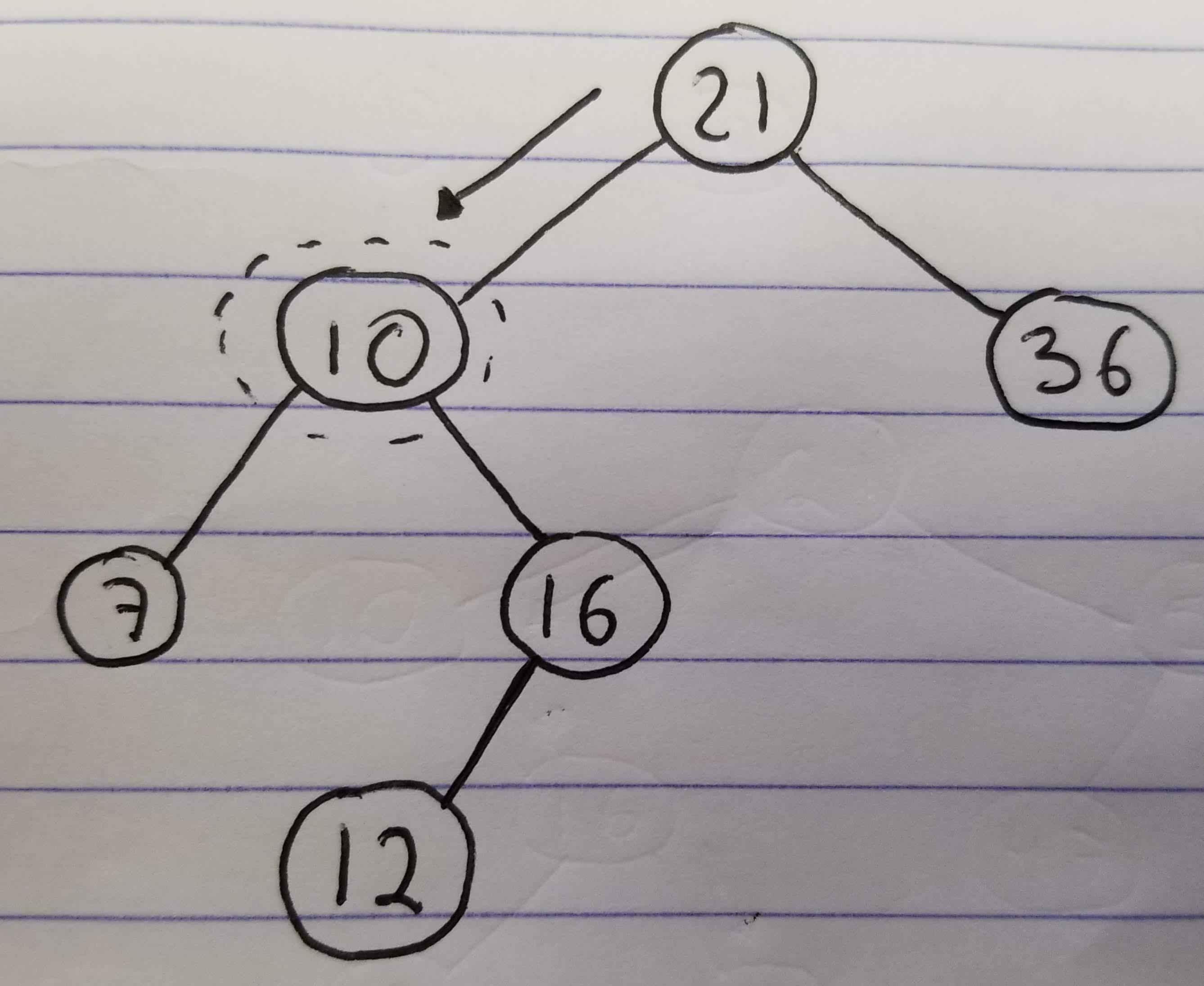
A little more complicated would be to delete a node with a single child:
- Find node
10 - Since
10is the left child of21, make7its left child instead
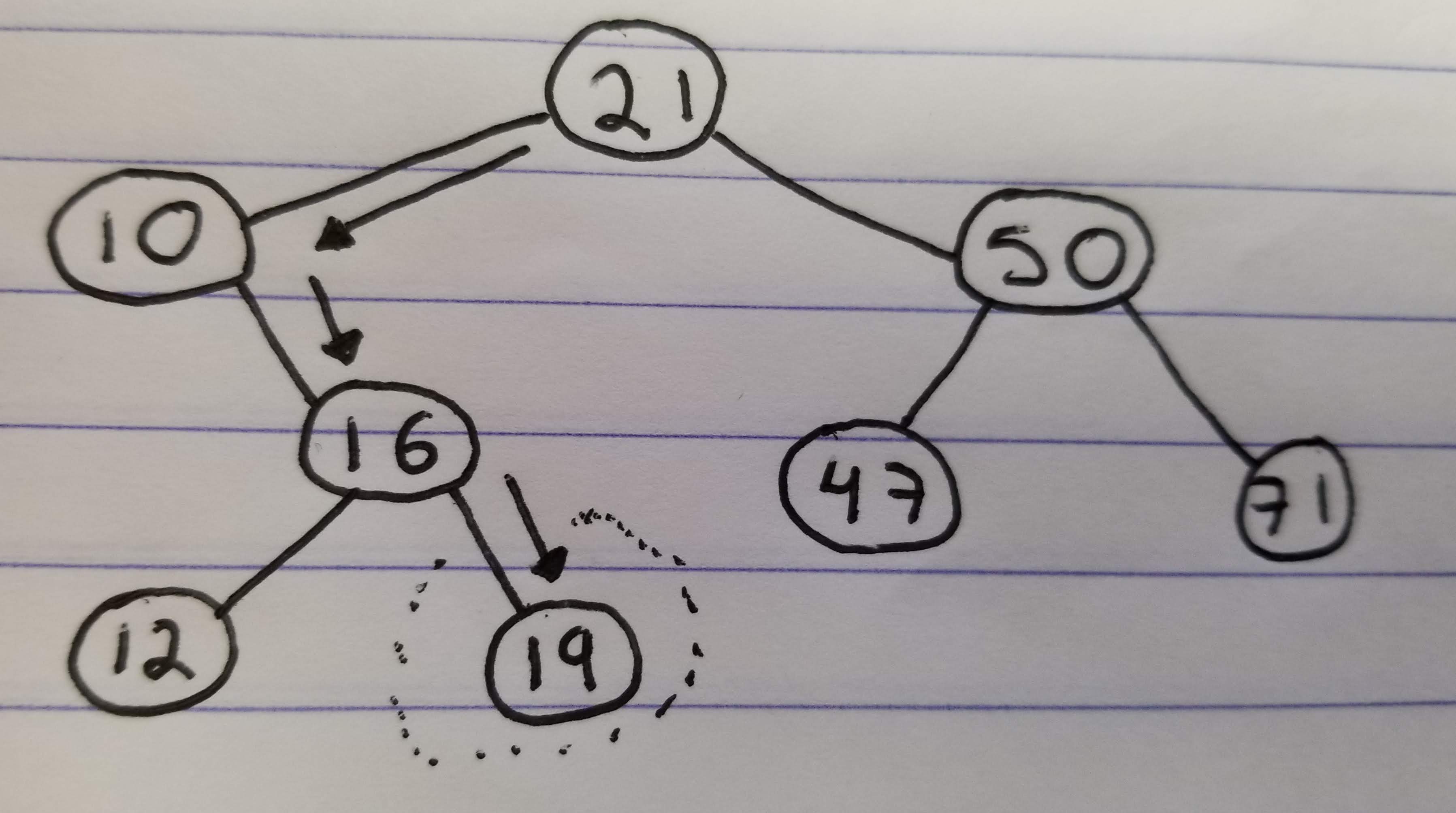
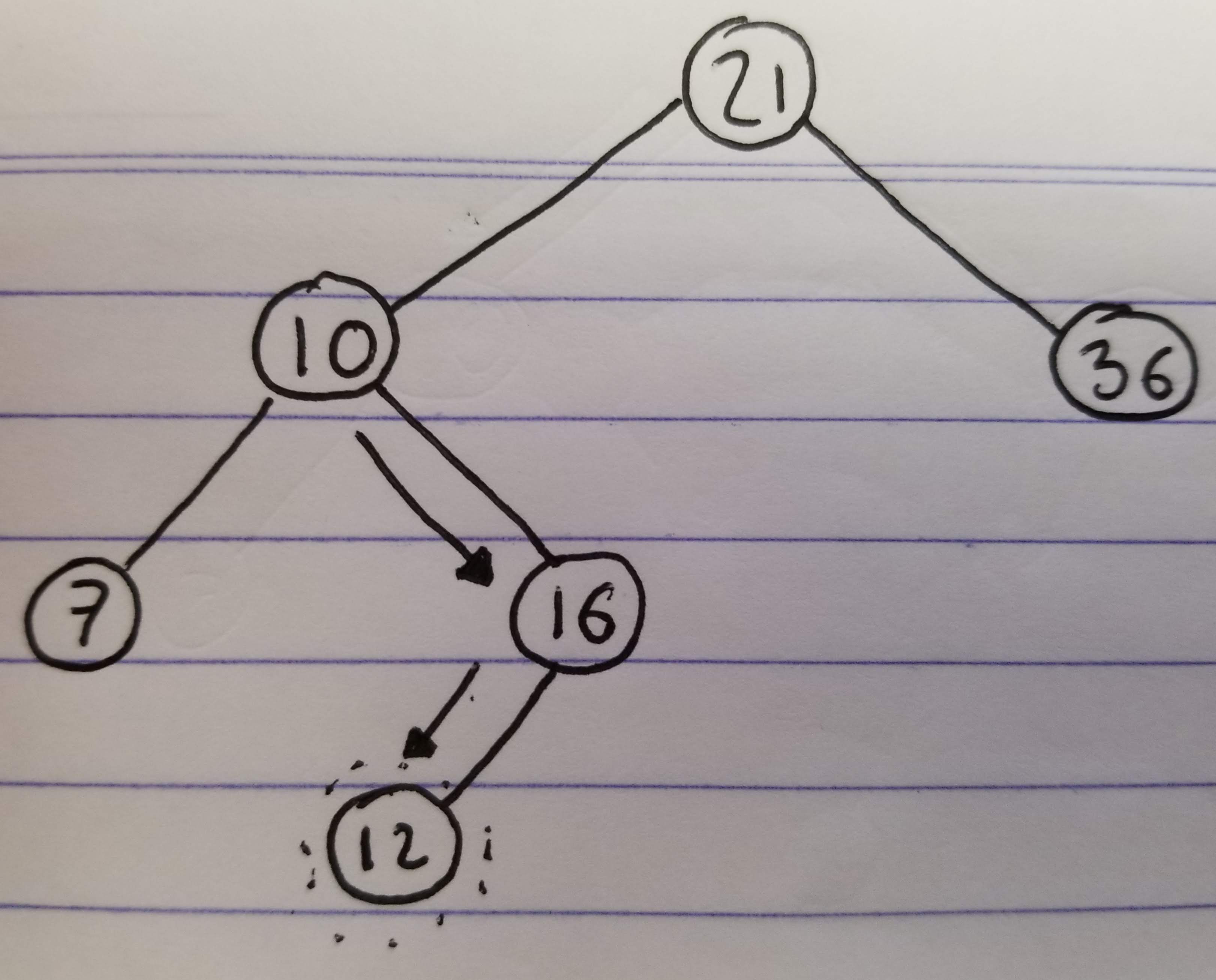
The most complicated case is the one where the node we want to delete has two children:
- Find node
10
- Go to the right child
- Go to the left until the last node is hit (
12)
- Replace the value of
10and12(10will end at the bottom) - Delete the node that has
10now (At this point it will have 0 or 1 children)
The code
Now that we know the algorithms, we can write the code. This is how it would look in JavasScript:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
class Bst {
// Create a node
_createNode(val, parent = null) {
return {
val: val,
parent: parent,
left: null,
right: null,
}
}
// Search for a value in this tree. If not found, returns
// the closest node (the node where the value would be
// inserted)
_findPosition(val) {
let current = this._root;
while (true) {
if (current.val === val) {
return current;
}
if (val > current.val && current.right) {
// The value we are searching for is greater.
// Continue on the right subtree
current = current.right;
} else if (val < current.val && current.left) {
// The value we are searching for is lower.
// Continue on the left subtree
current = current.left;
} else {
// No more tree to traverse
return current;
}
}
}
// Deletes the given node. The node must have at most
// one child
_deleteSimple(node) {
if (!node.left && !node.right) {
// No children, simple delete
if (!node.parent) {
this._root = null;
} else if (node.parent.right == node) {
node.parent.right = null;
} else {
node.parent.left = null;
}
} else {
// Single child, link the child to the parent
if (!node.parent) {
if (node.left) {
this._root = node.left;
node.left.parent = node.parent;
} else {
this._root = node.right;
node.right.parent = node.parent;
}
} else if (node.parent.right == node) {
if (node.left) {
node.left.parent = node.parent;
node.parent.right = node.left;
} else {
node.right.parent = node.parent;
node.parent.right = node.right;
}
} else {
if (node.left) {
node.left.parent = node.parent;
node.parent.left = node.left;
} else {
node.right.parent = node.parent;
node.parent.left = node.right;
}
}
}
}
// Search for a value in this tree
search(val) {
const found = this._findPosition(val);
if (found && found.val === val) {
return found;
}
}
// insert a value
insert(val) {
// The case where this is the first value
if (!this._root) {
this._root = this._createNode(val);
return;
}
// Search for the value. If it is found we don't need
// to do anything
let position = this._findPosition(val);
if (position.val === val) {
return;
}
// Insert the new value in the tree
if (position.val > val) {
position.left = this._createNode(val, position);
} else {
position.right = this._createNode(val, position);
}
}
// Delete a value from the tree
delete(val) {
// Search for the value. If it is not found we don't
// need to do anything
let node = this.search(val);
if (!node) {
return;
}
if (node.left && node.right) {
// Node has two children
let lowestRightNode = node.right;
while (lowestRightNode.left) {
lowestRightNode = lowestRightNode.left;
}
let tempVal = lowestRightNode.val;
lowestRightNode.val = node.val;
node.val = tempVal;
this._deleteSimple(lowestRightNode);
} else {
this._deleteSimple(node);
}
}
}
// Example of how to use it
let bst = new Bst();
bst.insert(4);
bst.insert(2);
bst.insert(3);
bst.search(3);
bst.delete(4);
console.log(bst._root);
programming javascript computer_science algorithms